1. Soal nomer5 ( SNMPT 2007, kode 341)
Jika x1 dan x2 adalah akar-akar dari persamaan (5 - 2 log x) log x = log 1000, maka nilai (x1)2 + (x2)2 adalah....(A) 0 (B) 10 (C) 100 (D) 1000 (E) 1100
Pembahasan:
5 log x - 2 (log x)2 = 3
5 log x - 2 (log x)2 - 3 = 0
2 (log x)2 - 5 log x + 3 = 0
(2 log x - 3)(log x - 1)=0
log x1 = 3/2 log x2 = 1
x1= x2=10
(x1)2 + (x2)2 =1000+100=1100
Jawaban: E
(Soal MatDas, SNMPT 2007, kode 341 nomer5)
2. Soal nomer6 ( SNMPT 2007, kode 341)
Persamaan kuadrat x2 + (a -1)x - (a -5)=0 mempunyai akar-akar x1 dan x2. Jika a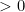 
dan x12.x2 + x1.x22=12, maka nilai dari a adalah....
(A) 5 (B) 6 (C) 7 (D) 8 (E) 9
Pembahasan:
x2 + (a -1)x - (a -5)=0
x1 + x2=1 - a
x1.x2 = 5 - a
x12.x2 + x1.x22= 12, a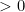
x1.x2(x1 + x2) = 12
(5 - a)(1 - a) = 12
a2 - 6a + 5 = 12
a2 - 6a -7 = 0
(a-7)(a+1)= 0
a = 7 atau a = -1 (TM)
Jawaban: C
(Soal MatDas, SNMPT 2007, kode 341 nomer6)
0 comments:
Post a Comment