Pembahasan SNMPTN 2012 - Matematika dasar kode 324

no. 1
Jika a dan b adalah bilangan bulat positif yang memenuhi a^b = 2²⁰ – 2¹⁹ , maka nilai a+b adalah....
(A) 3
(B) 7
(C) 19
(D) 21
(E) 23
Pembahasan:
a^b = 2²⁰ – 2¹⁹
=2¹⁹ (2 – 1)
=2¹⁹
a = 2 dan b = 19
sehingga: a+b=21

no. 2
Jika A, B, dan P, matriks berukuran 2x2, det(A) = 4, det(P)≠0, dan PA=BP, maka nilai det(A) – det(B) adalah...
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Pembahasan:
PA=BP
det(P). det(A)= det(P). det(B)
det(A)= det(B)
sehingga det(A) – det(B) = 0

no. 3
Jika p+1 dan p – 1 adalah akar-akar persamaan x²–4x + a=0, maka nilai a adalah:
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Pembahasan:
x₁ + x₂ = 4
2p = 4
P = 2
x₁ . x₂ = a
(2+1)(2 – 1) = a → a = 3

no. 4
Jika lima data memiliki rata-rata 12, median 12, modus 15, dan range (jangkauan) 7, maka data kedua setelah diurutkan adalah...
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
Pembahasan:
Rata-rata = 12 → a+b+c+d+e = 12(5)=60
Me = 12 → c = 12
j = e – a = 7 → e = 7 + a
Mo = 15
Deret tersebut adalah: 8 , 10 , 12 , 15 , 15

no. 5
Jika 240, 228, 216, ... adalah barisan aritmatika, maka suku bernilai kurang dari 12 yang muncul pertama kali adalah suku ke....
(A) 19
(B) 20
(C) 21
(D) 22
(E) 23
Pembahasan:
U_n < 12 240 + (n – 1)( – 12) < 12 (n – 1)( – 12) < 12 – 240 n – 1 < 19 n < 20 maka suku bernilai kurang dari 12 yang muncul pertama kali adalah suku ke 19

no. 6
Jika ^xlog y³ = 2, maka nilai ^ylog x⁴ adalah ...
(A) 1/8
(B) 3/8
(C) 8/3
(D) 6
(E) 8
Pembahasan:
^xlog y³ = 2
3. ^xlog y = 2
^xlog y= 2/3
^ylog x⁴ = 4. ^ylog x = 4. 3/2 = 6


no. 7
Jika diagram batang di bawah ini memperlihatkan frekuensi kumulatif hasil tes matematika siswa kelas XII, maka persentase siswa tang memperoleh nilai 8 adalah ....
(A) 12 %
(B) 15 %
(C) 20 %
(D) 22 %
(E) 80 %
Pembahasan:
(3/25).100 % = 12 %

no. 8
Jika 3x – 2y =8, 3y – 2z = 6, 3z – 2x = 4, maka nilai 4x – y + z adalah
(A) 12
(B) 14
(C) 18
(D) 22
(E) 26

Pembahasan:


no. 9
Jika persegi dengan panjang satu satuan dibagi menjadi lima persegi panjang dengan luas yang sama seperti ditunjukkan pada gambar, maka panjang ruas garis AB adalah....
(A) 3/5
(B) 1/4
(C) 2/5
(D) 1/2
(E) 1/5
Pembahasan: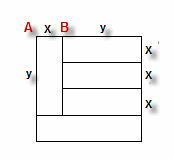

y + x = 1 dengan y = 3x
4x = 1 → x = 1/4
Sehingga AB =1/4

no. 10
Jika gambar dibawah ini adalah grafik fungsi kuadrat f dengan titik puncak (-2, 0) dan melalui titik (0,-4), maka nilai f(-5) adalah..
(A) – 7
(B) – 8
(C) – 9
(D) – 10
(E) – 11

Pembahasan:
y = a(x + 2) ²
-4 = a(0+2) ²
a = –1
sehingga f(–5) = –1 (–5+2) ²
= –1 (9) = –9

no. 11
Jika a adalah suku pertama, r adalah rasio, dan S_n=2(1 – 3ⁿ) adalah jumlah n suku pertama deret geometri, maka nilai a+5r adalah .....
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Pembahasan:
S_n=2(1 – 3^–n)
S₁=2(1 – 3^{– 1}) → S₁ = U₁=2(1 – (1/3)) = 4/3 =12/9
S₂=2(1 – 3^–2) → S₂ = 2(1 – (1/9))
U₁+ U₂=2(8/9) = 16/9 → U₂ = (16/9)– (4/3)= 4/9
r = (U₂/ U₁) = 1/3
a+5r= 4/3 + 5/3 = 3

no. 12
Semua nilai x yang memenuhi (x+1)(3x+2)≤(2x+2) adalah ....
(A) x ≥ (– 2/3)
(B) x ≤ 0
(C) x ≥ 1
(D) –1 ≤ x ≤ –2/3
(E) –1 ≤ x ≤ 0 atau x≥3
Pembahasan:
(x+1)(3x+2)≤(2x+2)
(x+1)(3x+2) – (2x +2) ≤0
(x+1)(3x+2 – 2)≤0
(x+1)(3x)≤0
Jawaban: –1 ≤ x ≤ 0

no. 13
Nilai maksimum fungsi objektif (tujuan) f(x,y) = 4x + y dengan kendala 2x + 5y ≤ 30, x ≥ 5, dan y ≥ 2 adalah ....
(A) 13
(B) 21
(C) 22
(D) 42
(E) 35
Pembahasan:
f(x,y) = 4x + y
f(5,2) = 4(5) + 2 = 22
f(10,2) = 40 + 2 = 42 → maksimum
f(5,4) = 4(5) + 4 = 24

no. 14
Jika f(x) = 5x – 3, g(x)= 3x + b dan g(f(1)) = 8, maka nilai g(1) adalah ......
(A) 5
(B) 6
(C) 8
(D) 11
(E) 12
Pembahasan:
f(1) = 5(1) – 3 = 2
g(f(1)) = 8
g(2)= 3(2) + b = 8 → b = 2
g(1)= 3(1) + 2 = 5

no. 15
Seorang Pengusaha menghasilkan produk A dan B yang masing-masing memberi keuntungan 8% dan 10% perbulan. Jika kedua jenis tersebut menghasilkan keuntungan Rp.904.000,00 setiap bulan dengan modal produk A Rp.4.800.000,00, maka modal pengusaha tersebut secara keseluruhan adalah....
(A) Rp.8.000.000,00
(B) Rp.9.000.000,00
(C) Rp.10.000.000,00
(D) Rp.11.000.000,0
(E) Rp.12.000.000,0
Pembahasan:

Posted in: Pembahasan, Pembahasan Matematika, SNMPTN