Panjang Vektor
Misalkan R adalah sebuah titik pada bidang dengan koordinat (x, y) dan r, maka r dapat disajikan dalam bentuk vektor kolom sebagai
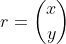
Panjang atau besar dari ruas garis berarah dilambangkan dengan |r|

Dari gambar di atas, didapat hubungan:
OR2 = OA2 + OB2
OR2 = x2 + y2
OR = √(x2 + y2)
Dengan demikian, panjang adalah:
adalah:
|OR| = √(x2 + y2)
Jadi, besar atau panjang vektor r dapat ditentukan dengan rumus:
|r| = √(x2 + y2)
Misalkan titik R mempunyai koordinat (x, y, z) dan mewakili vektor r, maka vektor r dapat dinyatakan dalam bentuk vektor kolom sebagai
mewakili vektor r, maka vektor r dapat dinyatakan dalam bentuk vektor kolom sebagai
 .
.
Panjang atau besar ruas garis berarah ditulis sebagai |
ditulis sebagai | | atau OR.
| atau OR.

Berdasarkan gambar di atas diperoleh hubungan:
OR2 = OD2 + DR2 ...................... (1)
Sedangkan OD2 = OA2 + OB2
OD2 = x2 + y2
dan DR2 = z2
Substitusi OD2 dan DR2 ke persamaan (1) diperoleh
OR2 = x2 + y2 + z2
Dengan demikian

Jadi, besar atau panjang vektor r (x, y, z) dapat ditentukan dengan rumus

Contoh:
Diketahui vektor-vektor
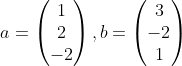
Hitunglah|2a - b|
Jawab:
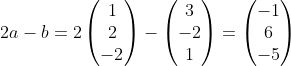
|2a - b| = √[(-1)2 + 62 + (-5)2)]= √(1+36+25)= √62
Jadi, panjang vektor 2a - b adalah |2a - b| = √62 satuan panjang
Misalkan R adalah sebuah titik pada bidang dengan koordinat (x, y) dan r, maka r dapat disajikan dalam bentuk vektor kolom sebagai
Panjang atau besar dari ruas garis berarah dilambangkan dengan |r|

Dari gambar di atas, didapat hubungan:
OR2 = OA2 + OB2
OR2 = x2 + y2
OR = √(x2 + y2)
Dengan demikian, panjang
|OR| = √(x2 + y2)
Jadi, besar atau panjang vektor r dapat ditentukan dengan rumus:
|r| = √(x2 + y2)
Misalkan titik R mempunyai koordinat (x, y, z) dan
Panjang atau besar ruas garis berarah

Berdasarkan gambar di atas diperoleh hubungan:
OR2 = OD2 + DR2 ...................... (1)
Sedangkan OD2 = OA2 + OB2
OD2 = x2 + y2
dan DR2 = z2
Substitusi OD2 dan DR2 ke persamaan (1) diperoleh
OR2 = x2 + y2 + z2
Dengan demikian

Jadi, besar atau panjang vektor r (x, y, z) dapat ditentukan dengan rumus

Contoh:
Diketahui vektor-vektor
Hitunglah|2a - b|
Jawab:
|2a - b| = √[(-1)2 + 62 + (-5)2)]= √(1+36+25)= √62
Jadi, panjang vektor 2a - b adalah |2a - b| = √62 satuan panjang
















7 comments:
amazing
Sub
kok ga bisa di copast yaa kak
kok ga bisa di copast yaa kak
maaf sedikit mengoreksi itu hasil 2a-b apa benar akar 72? bukanya hasil jumlah dari 1+36+25 adalah 62 ya.
Yupsss...
Hasilnya √62.
Maaf kurang teliti, efek mengantuk. Skrg sudah diperbaiki.
Terima kasih untuk koreksinya.
kok tidak bisa di copas ya??
Post a Comment